如何通过卖期权,在牛市管理闲置资金
牛市中,持有闲置资金是一种折磨!担心踏空,又怕追高被套。
最近接触期权的卖方策略(Cash-Secured Put和Covered Call),发现是个闲置现金管理的利器。
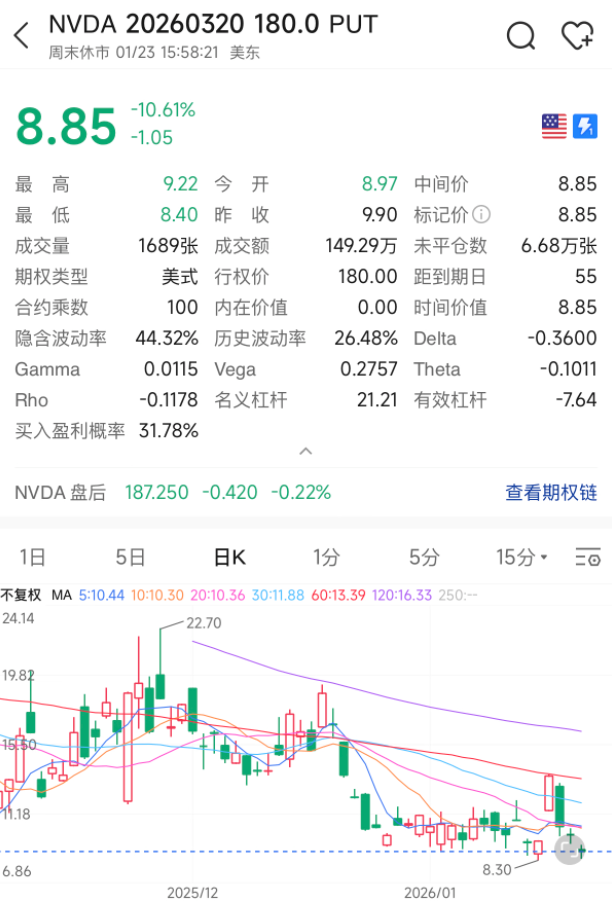
以卖出一张英伟达20260320到期的put为例(见下图),
- 承诺:我备好 $18,000 美元现金,承诺2个月内无论英伟达跌到多少,我都愿意以 $180 买入。
- 对价:作为交换,对手方需立即支付我 $8.85 的权利金(合约面值 $885,$8.85是每股权利金,一份合约对应100股)。
卖方盈亏分类讨论:
- 情形1,股价跌破 $180: 对方行权。我以 $180 接盘,扣除已收到的权利金,实际成本约为 $171.15。相比当前市价($187.25),我相当于打了92折买到了心仪的资产。
- 情形2,股价在 $180 以上: 对方不行权。我白赚 $885 权利金。这笔闲置资金的年化收益率可达 37.9%(885/(18000-885)/55*365+3.6%美债收益率)。
双赢,就是要赢两次!要么我以37.9%的年化收益率白赚权利金,要么以92折的价格买到心仪的资产。
这就是Cash-Secured Put策略:备足现金,在恰当的时机,以你愿意接盘的价格,卖出看跌期权PUT。
但这有个关键问题,什么是恰当的时机?作为卖方,肯定希望能在期权价格最高的时候卖出。
从上图看,期权价格每天的波动非常大。同样是这张180的put,短短两天就从 $13.55 跌到 $8.85。意味着,如果提前2天卖,年化收益率能到55.7%,两者差了17.8%!
期权价格是怎么波动的?
这是个诺奖级别的问题,Black-Scholes公式提供了解答。为了理解这个公式,我们先要理解软件上那些希腊字母的物理含义。
- Delta $\Delta$:
- 定义:期权价格 $V$ 对标的资产价格 $S$ 的一阶偏导
- 含义:$\Delta=-0.36$ 意味着,股价每上涨 $1,期权价格会下跌 $0.36。因此卖出1份put,在价格波动上,可视为做多36股英伟达。
- Gamma $\Gamma$
- 定义:期权价格 $V$ 对标的资产价格 $S$ 的二阶偏导
- 含义:衡量期权价格曲线的弯曲程度。$\Gamma$越大,说明$\Delta$随股价波动的漂移速度越快。这个学问很深,以后会专门讲。
- Theta $\Theta$
- 定义:期权价格 $V$ 对时间 $t$(通常指剩余期限 $\tau$)的一阶偏导
- 含义:衡量在其他条件不变的情况下,期权价值随时间流逝而缩水的速率。$\Theta=-0.1011$ 意味着,如果其他条件不变,作为卖方,我每天会将 $0.1011 的权利金收入囊中。一般来说越临近到期,流逝速度越快,因为行权的概率快速坍缩。
- Vega $\nu$
- 定义:期权价格 $V$ 对波动率 $\sigma$ 的一阶偏导
- 含义:$\nu=0.25$ 如果有什么突发事件导致市场恐慌,隐含波动率从30%跳升到40%,期权价格会上涨 $2.5。
- Rho $\rho$
- 定义:期权价格 $V$ 对无风险利率 $r$ 的一阶偏导数
- 含义:这项的影响较小,一般忽略。
有了上面的基础,我们可以写出期权价格的变动公式:
\[\Delta V \approx \underbrace{\Delta \cdot dS}_{\text{方向性损益}} + \underbrace{\frac{1}{2} \Gamma \cdot (dS)^2}_{\text{凸性收益}} + \underbrace{\Theta \cdot dt}_{\text{时间价值损益}} + \underbrace{\nu \cdot d\sigma}_{\text{波动率风险损益}} + \underbrace{\rho \cdot dr}_{\text{无风险利率项}}\]这个公式给期权卖方指明了收益的来源:
- $\Theta$:时间价值损益,随着时间流逝,权利金每天都自动流入我们的口袋。
- $\nu$:波动率风险损益,如果能在高波动率(通常是市场恐慌)时期卖期权,能享受到一个不错的溢价。比如上图中,期权价格差异巨大,是因为1月20日,Trump以格陵兰岛争端为由,对各国征收额外关税,导致市场恐慌。
但作为卖家,这个公式也有让人讨厌的地方,$\Gamma$。期权是零和博弈,我们通过$\Theta$来赚买家的钱,买家也必然有方法赚我们的钱,那就是 $\Gamma$。
为了理解$\Theta$与$\Gamma$之间的对价关系,我用delta中性策略来举例。
Delta中性策略,就是要构建一个delta=0的投资组合。如果你还记得delta的定义,这意味着你的账户不会受到股价波动的影响!同时,当Delta=0时,$\Theta$ 与 $\Gamma$ 的关系是:
\[\Theta + \frac{1}{2} \sigma ^2 S^2 \Gamma = 0\]为了实现Delta中性,买家可以如此操作(请注意,针对看跌期权put,由于Gamma的存在,股价上涨delta会变小,股价下跌delta会变大):
| 阶段 | 市场状态 | 期权 Delta (1张=100股) | 正股持有量 (Delta +1/股) | 组合总 Delta | 仓位状态 | 说明 |
|---|---|---|---|---|---|---|
| 1. 初始构建 | 股价 S | -0.36 x 100 = -36 | 买入 36 股 | 0 | — | 建立初始中性对冲 |
| 2. 股价上涨 | 股价 S + 1 | -0.32 x 100 = -32 | 持有 36 股 | +4 | 组合变为轻微看多 | 股价上涨导致Delta向正向偏移 |
| 3. 动态调仓 | 股价 S + 1 | -32 | 卖出 4 股,余 32股 | 0 | 卖出 4 股正股 | 实现“高抛”利润 |
| 4. 股价下跌 | 股价 S | -0.36 x 100 = -36 | 持有 32 股 | -4 | 组合变为轻微看空 | 股价下跌时,Gamma使得Delta负向偏移 |
| 5. 再次调仓 | 股价 S | -36 | 买入 4 股,回 36股 | 0 | 买入 4 股正股 | 实现“低吸”建仓,重回Delta中性 |
可以观察到,在维持delta中性策略的过程中,买家自动完成了一次“高抛低吸”的操作。我们可以看看如果卖家同样执行这个操作,会发生什么:
| 阶段 | 市场状态 | 期权 Delta (1张=100股) | 正股持有量 (Delta +1/股) | 组合总 Delta | 仓位状态 | 说明 |
|---|---|---|---|---|---|---|
| 1. 初始构建 | 股价 S | +0.36 x 100 = +36 | 卖空 36 股 | 0 | — | 建立初始中性对冲 |
| 2. 股价上涨 | 股价 S + 1 | +0.32 x 100 = +32 | 卖空 36 股 | -4 | 组合变为轻微看空 | 股价上涨时,负Gamma使 Delta负向偏移 |
| 3. 动态调仓 | 股价 S + 1 | +32 | 买入 4 股平仓,余卖空 32 股 | 0 | 高位买入 4 股 | 被迫“追涨” |
| 4. 股价下跌 | 股价 S | +0.36 x 100 = +36 | 卖空 32 股 | +4 | 组合变为轻微看多 | 股价下跌时,负Gamma使Delta正向偏移 |
| 5. 再次调仓 | 股价 S | +36 | 卖出 4 股建仓,回卖空 36 股 | 0 | 低位卖出 4 股 | 被迫“杀跌” |
你会发现,买家自动地“低吸高抛”,而卖家则是被迫“低抛高吸”。换句话说,假设市场里只有卖方和买方两个玩家。卖方通过$\Theta$剥削买方,赚时间流逝的钱;买方通过$\Gamma$剥削卖方,赚股价波动的钱。买方是每天向卖方支付了门票费$\Theta$,博取从股价波动赚钱的可能性。
上面的分析,有助于我们理解期权的博弈机制。但Cash-Secured Put策略很简单,不理解上面的概念也没问题,只需要在实践中遵循一些基本原则:
- 备足现金: 永远不要为了高保费去加杠杆。
- 选择高隐含波动率(IV)场景: 在市场恐慌、IV 处于高位时卖出。
- 择股重于择时: 只有在你愿意长期持有的标的上进行操作。最坏的结果不过是“打折买入好公司”。